The Resistor Cube

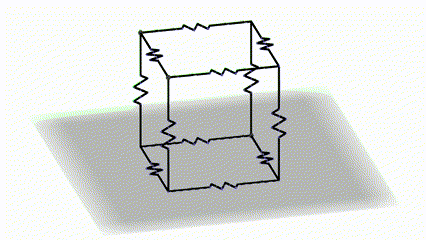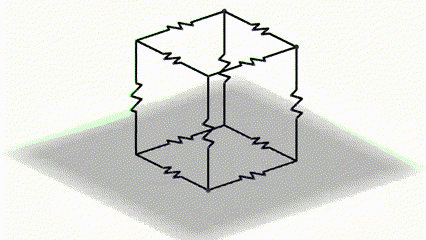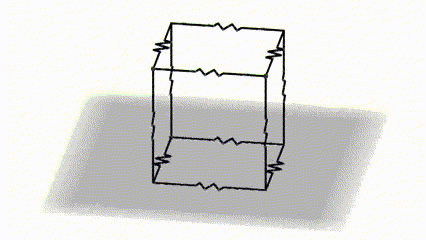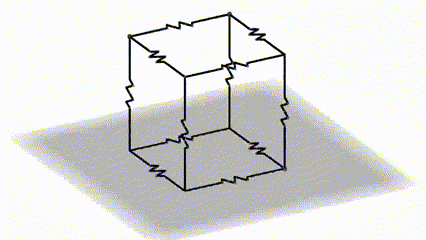
This is a classic high school problem where 12 identical resistors are connected in a circuit so that each resistor occupies the edge of a cube. The question is to calculate the equivalent resistance of such a circuit between points A and B.

To obtain the requested equivalent resistance, we will use the existing symmetry characteristic in the presented scheme and the premise that the potential is established by the electric field, which is conservative, and independent of the path.

Step 1:

Let’s short-circuit the two vertices of the two faces of the cube, the top and the bottom, as shown in the figure below.

Step 2:

Now the scheme will be flat as shown in the figure below. Notice that the resistors are nested, highlighting the parallel branch associations.

Step 3:

Now the redesign is done, with the parallel horizontal branches replaced by branches with the respective equivalent resistances whose value is trivial, that is, half of R.

Step 4:

Finally, the simplification of the intermediate vertical parallel branches is done in the same way, that is, replaced by a branch with equivalent resistance R/2. This branch is now bridging the loop.

Step 5:

Now the simplification of the branches with resistances in series, whose value is obtained by the simple sum of the resistances.

Step 6:

This step is a simple trick to solve, alternating the branches connected to point B and at the same time eliminating the bridge branch.

Result of plausible circuit modification process.

Step 7:

Once the circuit has been reduced to two associated resistors, the equivalent resistance formula of two parallel resistors is immediately applied.

Step 8:

Here we have the application of the formula corresponding to the association of two resistors in parallel.

⚠️In step 6 there will be no problems when replacing the resistors in the way it was done, since the symmetry presented in this step allows eliminating the bridge resistor without altering a total current that passes through the circuit, and that with this we will obtain in any case the resistance requested equivalent.